Tutorial

This tutorial will describe how to set up and solve optimization problems in python.

Move arm to joint target

Full source code: python_examples/arm_to_joint_target.py

The following script will plan to get the right arm to a joint-space target. It is assumed that the robot’s current state is the start state, so make sure you set the robots DOFs appropriately.

The optimization will go very fast (the main waiting time is from loading the robot files). To see the optimization in action, run the script with the option --interactive=True. The optimization will pause at every iteration and plot the current trajectory and contacts. Press ‘p’ to unpause and continue.

import argparse
parser = argparse.ArgumentParser()
parser.add_argument("--interactive", action="store_true")
args = parser.parse_args()

import openravepy
import trajoptpy
import json
import time

env = openravepy.Environment()
env.StopSimulation()
env.Load("robots/pr2-beta-static.zae")
env.Load("../data/table.xml")

trajoptpy.SetInteractive(args.interactive) # pause every iteration, until you press 'p'. Press escape to disable further plotting
robot = env.GetRobots()[0]

joint_start = [-1.832, -0.332, -1.011, -1.437, -1.1  , -2.106,  3.074]
robot.SetDOFValues(joint_start, robot.GetManipulator('rightarm').GetArmIndices())

joint_target = [0.062, 1.287, 0.1, -1.554, -3.011, -0.268, 2.988]


request = {
  "basic_info" : {
    "n_steps" : 10,
    "manip" : "rightarm", # see below for valid values
    "start_fixed" : True # i.e., DOF values at first timestep are fixed based on current robot state
  },
  "costs" : [
  {
    "type" : "joint_vel", # joint-space velocity cost
    "params": {"coeffs" : [1]} # a list of length one is automatically expanded to a list of length n_dofs
    # also valid: [1.9, 2, 3, 4, 5, 5, 4, 3, 2, 1]
  },
  {
    "type" : "collision",
    "params" : {
      "coeffs" : [20], # penalty coefficients. list of length one is automatically expanded to a list of length n_timesteps
      "dist_pen" : [0.025] # robot-obstacle distance that penalty kicks in. expands to length n_timesteps
    },    
  }
  ],
  "constraints" : [
  {
    "type" : "joint", # joint-space target
    "params" : {"vals" : joint_target } # length of vals = # dofs of manip
  }
  ],
  "init_info" : {
      "type" : "straight_line", # straight line in joint space.
      "endpoint" : joint_target
  }
}
s = json.dumps(request) # convert dictionary into json-formatted string
prob = trajoptpy.ConstructProblem(s, env) # create object that stores optimization problem
t_start = time.time()
result = trajoptpy.OptimizeProblem(prob) # do optimization
t_elapsed = time.time() - t_start
print result
print "optimization took %.3f seconds"%t_elapsed

from trajoptpy.check_traj import traj_is_safe
prob.SetRobotActiveDOFs() # set robot DOFs to DOFs in optimization problem
assert traj_is_safe(result.GetTraj(), robot) # Check that trajectory is collision free

Every problem description contains four sections: basic_info, costs, constraints, and init_info (i.e., initialization info).

Here, there are two cost components: joint-space velocity, and the collision penalty. There is one constraint: the final joint state.

Note

Why do we use a collision cost, rather than a constraint? In the sequential convex optimization procedure, constraints get converted into costs–specifically, 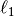penalties (see the paper). So the difference between a constraint and an 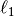cost is that for a constraint, the optimizer checks to see if it is satisfied (to some tolerance), and if not, it jacks up the penalty coefficient. The thing about collisions is that it’s often necessary to violate the safety margin, e.g. when you need to contact an object. So you’re best off handling the logic yourself of adjusting penalties and safety margins, based on your specific problem.

See Collision costs for more info on the collision penalty.

Move arm to pose target

Full source code: python_examples/arm_to_cart_target.py

Next, let’s solve the same problem, but instead of specifying the target joint position, we’ll specify the target pose.

Now we use a pose constraint instead of a joint constraint:

  {
    "type" : "pose", 
    "params" : {"xyz" : xyz_target, 
                "wxyz" : quat_target, 
                "link": "r_gripper_tool_frame",
                "timestep" : 9
                }
                 
  }

Initialize using collision-free IK:

manip = robot.GetManipulator("rightarm")
init_joint_target = ku.ik_for_link(hmat_target, manip, "r_gripper_tool_frame",
    filter_options = openravepy.IkFilterOptions.CheckEnvCollisions)

...

  "init_info" : {
      "type" : "straight_line", # straight line in joint space.
      "endpoint" : init_joint_target.tolist() # need to convert numpy array to list
  }

Increasing reliability with multiple initializations

Whether you use a straight-line initialization, stationary initialization, or something else, there’s a decent chance that the local optimization will converge to a local minimum which is not collision-free. The solution to this problem is to use multiple initializations. The simplest alternative initialization is of the form Start-Waypoint-Goal, i.e., you linearly interpolate between the start state and a waypoint, and then you linearly interpolate between the waypoint and the goal. You can see this strategy in benchmark.py, which uses four waypoints. Using this strategy, the algorithm solves 100% of 204 planning problems in the three provided scenes (tabletop, bookshelves, and kitchen_counter).

All in all, there are several ways to initialize:

• Stationary: Initialize with the trajectory that stands still for n_steps timesteps.

  "init_info" : {
      "type" : "stationary"
  }
  

• With a given trajectory:

  "init_info" : {
      "type" : "given_traj"
      "data" : [[ 0.   ,  0.   ,  0.   ],
                 [ 0.111,  0.222,  0.333],
                 [ 0.222,  0.444,  0.667],
                 [ 0.333,  0.667,  1.   ],
                 [ 0.444,  0.889,  1.333],
                 [ 0.556,  1.111,  1.667],
                 [ 0.667,  1.333,  2.   ],
                 [ 0.778,  1.556,  2.333],
                 [ 0.889,  1.778,  2.667],
                 [ 1.   ,  2.   ,  3.   ]]
  }
  

  data must be a 2d array with n_steps rows, and the first row must be the robot’s current DOF values

• With a straight line in configuration space.

  "init_info" : {
      "type" : "given_traj"
      "endpoint" : [ 1.   ,  2.   ,  3.   ]
  }
  

  The robot’s DOF values are used for the start point of the line.

Rolling your own costs and constraints in python

Full source code: python_examples/this_side_up.py

This next script shows how you can easily implement your own costs and constraints. The constraint we consider here says that a certain vector defined in the robot gripper frame must point up (in the world coordinates). For example, one might imagine that the robot is holding a glass of water, and we don’t want it to spill.

The basic setup of the problem is similar to the previous examples. Before getting to the python constraint functions, we’ll add some constraints to the problem in the json file, including a cartesian velocity constraint.

We set a pose constraint at the end of the trajectory. This time, we ignore the rotation (by setting rot_coefs = [0,0,0]).

  {
    "type" : "pose", 
    "params" : {"xyz" : xyz_target, 
                "wxyz" : [1,0,0,0],  # unused
                "link": "r_gripper_tool_frame",
                "rot_coeffs" : [0,0,0],
                "pos_coeffs" : [10,10,10]
                }
                 
  },

We also add a constraint on the end-effector displacement at each step:

  {
    "type" : "cart_vel",
    "name" : "cart_vel",
    "params" : {
        "max_displacement" : .05,
        "first_step" : 0,
        "last_step" : n_steps-1, #inclusive
        "link" : "r_gripper_tool_frame"
    },
  }

The parameter "max_displacement : .05" means the position of the link (r_gripper_tool_frame) moves by less than .05 in each timestep, for each component (x,y,z).

Now, let’s look at the user-defined costs and constraints. We define an vector-valued error function f(x), and the Jacobian of this function dfdx(x). f(x) returns the x and y components of the transformed vector (which both equal zero if the vector points up).

def f(x):
    robot.SetDOFValues(x, arm_inds, False)
    return tool_link.GetTransform()[:2,:3].dot(local_dir)
def dfdx(x):
    robot.SetDOFValues(x, arm_inds, False)
    world_dir = tool_link.GetTransform()[:3,:3].dot(local_dir)
    return np.array([np.cross(joint.GetAxis(), world_dir)[:2] for joint in arm_joints]).T.copy()

We add these error functions to the problem as constraints (i.e., that error should equal 0) with the following lines:

    for t in xrange(1,n_steps):    
        if args.diffmethod == "numerical":
            prob.AddConstraint(f, [(t,j) for j in xrange(7)], "EQ", "up%i"%t)
        elif args.diffmethod == "analytic":
            prob.AddConstraint(f, dfdx, [(t,j) for j in xrange(7)], "EQ", "up%i"%t)

As you can see, we can provide only the function f (which will be numerically differentiated internally), or we can also provide the function and its analytic derivative. Note that in both calls to AddConstraint, we pass in the following parameter: [(t,j) for j in xrange(7)]. This argument is telling the optimizer which variables the provided function should be applied to. This parameter must be a list of ordered pairs (timestep, dof). These ordered pairs specify which trajectory variables make up the input vector for your provided functions. For example, we add a “up” cost at timestep t=3 by providing the indices [(3,0), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6)]. Then the optimizer knows that this constraint function should be applied to the vector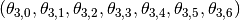

Similarly to the way we added those constraints, we can also add the error functions as costs, as a hinge, abs, or squared loss, using the function TrajOptProb.AddErrCost. Or, we can provide a single scalar-valued cost function by using the function TrajOptProb.AddCost.

Optimizing the base position and torso height

This next example shows how to jointly optimize over the base and torso degrees of freedom of a mobile robot, as well as the arms. This program considers a trajectory with one timestep, and start_fixed=False, so it is really just doing collision-aware numerical IK. You can optimize over a trajectory containing all of these degrees of freedom by setting n_steps. basic_info is set as follows:

        "basic_info" : {
            "n_steps" : 1,
            "manip" : "active",
            "start_fixed" : False
        },

Note that manip="active", which makes the selects the degrees of freedom of the optimization problem based on the degrees of freedom of the robot, which we set earlier:

robot.SetActiveDOFs(np.r_[robot.GetManipulator("rightarm").GetArmIndices(), 
                          robot.GetJoint("torso_lift_joint").GetDOFIndex()], 
                    rave.DOFAffine.X + rave.DOFAffine.Y + rave.DOFAffine.RotationAxis, [0,0,1])

Numerical IK is very unreliable since the forward kinematics function is so nonlinear. Therefore, we do a series of random initializations:

    # randomly select joint values with uniform distribution over joint limits
    lower,upper = robot.GetActiveDOFLimits()
    lower = np.clip(lower, -np.pi, np.pi) # continuous joints have huge ranges, so we clip them to [-pi, pi]
    upper = np.clip(upper, -np.pi, np.pi) # to avoid poor numerical conditioning
    rands = np.random.rand(len(lower))
    dofvals_init = lower*rands + upper*(1-rands)
    # we'll treat the base pose specially, choosing a random angle and then setting a reasonable
    # position based on this angle
    angle_init = np.random.rand() * 2*np.pi
    x_init = xyz_targ[0] - .5*np.cos(angle_init)
    y_init = xyz_targ[1] - .5*np.sin(angle_init)    
    dofvals_init[-3:] = [x_init, y_init, angle_init]

Note that you can also optimize over whole trajectories involving the base and torso. For example, see the section on sensor data.

Walking with humanoid robot

Note

To run the example script, you’ll need to download the test data and build with the CMake option BUILD_HUMANOIDS=ON.

See python_examples/drc_walk.py for a simple example of planning footsteps with the Atlas robot model (for DARPA robotics challenge).

The walk cycle consists of the following four phases, each of which is motion-planned independently:

1. Shift center of mass so it’s over right foot
2. While keeping center of mass over right foot, swing left foot forward
3. Shift center of mass so it’s over left foot
4. While keeping center of mass over left foot, swing right foot forward

These planning problems involve pose constraints, as well as a “ZMP” constraint, which constrains the robot’s center of mass to lie above the convex hull of the one or two planted feet. This gait will provide a stable walk in the quasi-static regime that the robot moves very slowly (i.e., the forces and torques needed to accelerate the robot are negligible compared with the weight of the robot).

Obstacle geometry from sensor data

Note

To run the example script, you’ll need to download the test data and build with the CMake option BUILD_CLOUDPROC=ON.

We’ll consider three different ways of representing the geometry of the environment:

1. as a collection of boxes or spheres

The advantage is that the preprocessing of the input point cloud or voxel data is very simple. The disadvantages are that (a) this representation is usually slow to collision check against, (b) for the purposes of trajectory optimization, the contact normals aren’t very informative about how to get out of collision

2. as a mesh

There are a variety of algorithms for reconstructing surfaces from point clouds. The included script uses the simplest type of surface generation algorithm, which forms a mesh out of a single depth image by connecting neighboring points in the pixel array. After constructing the mesh, we decimate it, i.e., simplify it by iteratively merging vertices.

3. convex decomposition

The idea of convex decomposition is to break down a 3D shape into a set of convex pieces. The resulting convex decomposition allows fast collision checking and good surface normals. We use Khaled Mammou’s Hierarchical Approximate Convex Decomposition (HACD) code.

Here is a table summarizing the tradeoffs:

	boxes	mesh	convex decomp
construction cost	low	med	high
coll. check speed	low	med	high
normal quality	low	med	high

We highly recommend using meshes or convex decomposition with trajopt, since these representations will perform far better than boxes with regard to speed and likelihood of finding a solution.

A demonstration of using all three of these methods can be found in python_examples/kinect_drive_and_reach.py. After driving a PR2 robot to several positions in an office, we acquired a single point cloud (xyz + rgb) from the robot’s head-mounted Kinect and saved it, along with the joint state and camera transformation. For each scene, we have annotated a target pose for the right gripper (pose_target.txt). We then plan a trajectory which simultaneously moves the right arm, torso, and base (11 = 7 + 1 + 3 DOF) to reach this target.

To use the mesh or convex decomposition for collision geometry, we first construct a mesh from the point cloud.

def generate_mesh(cloud):
    cloud = cloudprocpy.fastBilateralFilter(cloud, 15, .05) # smooth out the depth image
    cloud = remove_floor(cloud) # remove points with low height (in world frame)
    big_mesh = cloudprocpy.meshOFM(cloud, 3, .1) # use pcl OrganizedFastMesh to make mesh
    simple_mesh = cloudprocpy.quadricSimplifyVTK(big_mesh, .02) # decimate mesh with VTK function
    return simple_mesh

Note that the module cloudprocpy is a set of python bindings to the Point Cloud Library (PCL), plus a few functions from other libraries.

For convex decomposition, we call a function to break the mesh into a set of convex pieces

convex_meshes = cloudprocpy.convexDecompHACD(big_mesh,30)

The second parameter (30) relates to the allowed concavity of each almost-convex subset; see the docstring for more information.